묻고답하기
고수 여러분, 도와 주세요.
2009.08.12 22:41
아래는 위 소스입니다.
| |||||||||||||||||||||||||||
그런데 이것을 제 홈페이지 페이지나 게시판에 넣으면 다음과 같이 나타납니다.
페이지에 넣으면 아래와 같이 정상적으로 나타납니다.
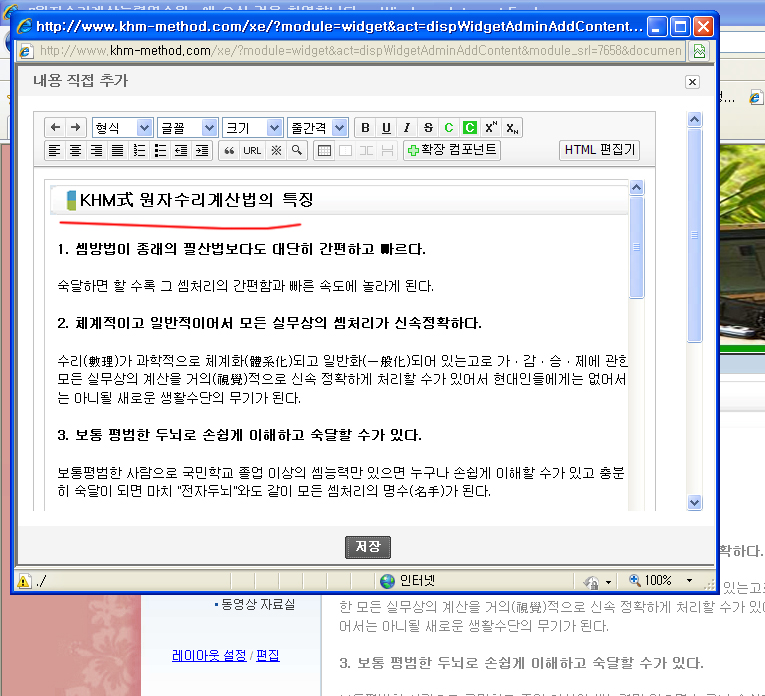
그런데 위 [저장] 단추를 누르면 아래와 같이 비정상적으로 백 이미지가 밑에 이중으로 나타납니다.
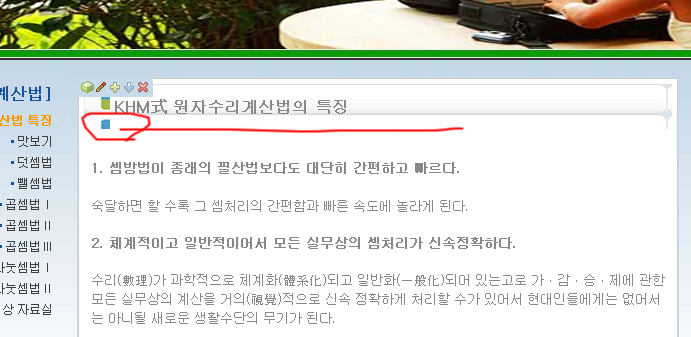
화면 아래 [저장] 단추를 누르면 아래와 같이 비정상입니다.
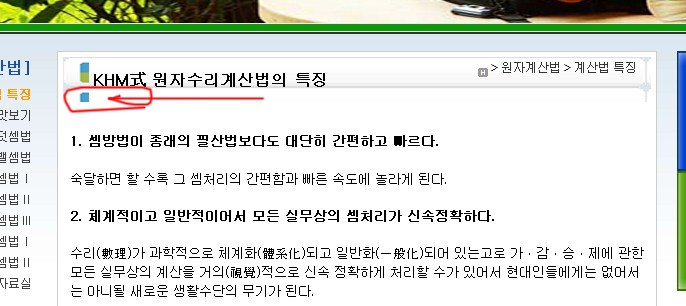
그런데 다시 수정모드로 들어가면 아래와 같이 정상적으로 보여집니다.
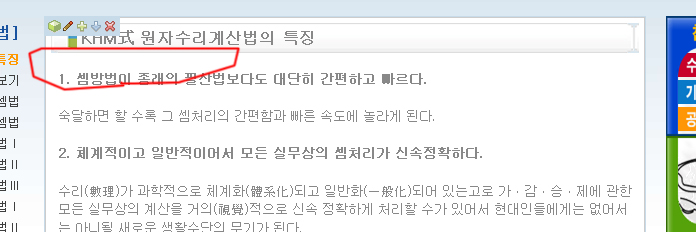
위 동일한 소스를 이곳 제로보드 게시판에 넣으면 아래와 같이 정상적입니다.
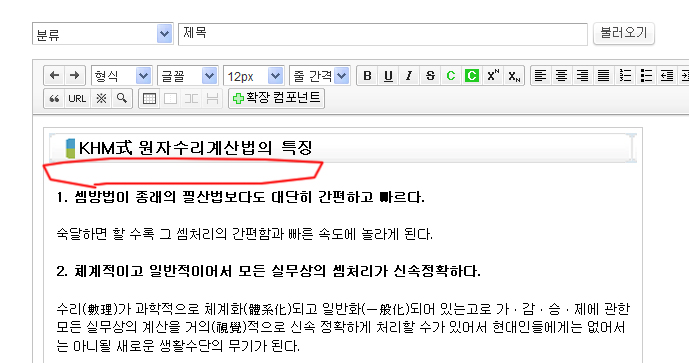
그런데 이것을 제 홈페이지 게시판에 넣으면 비정상적으로 나타나 보입니다.
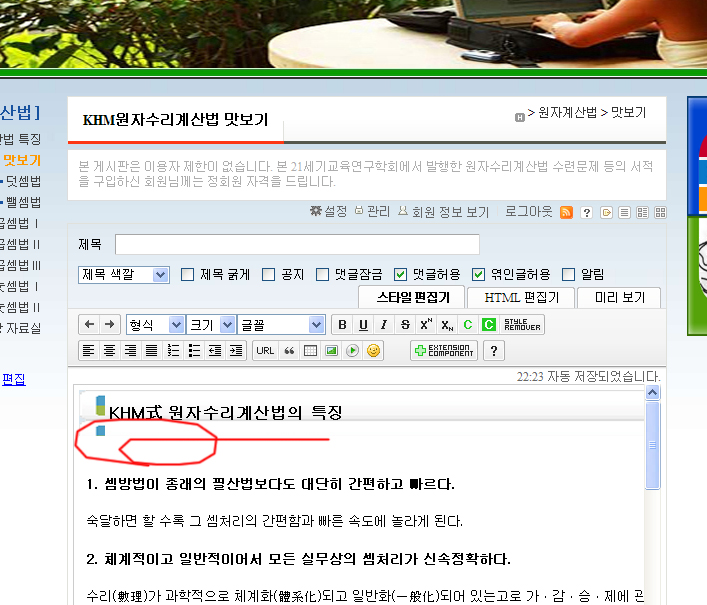
이것이 무엇에 의한 문제일까요?
XEPRESSEDITOR 문제일까요?
이것이 문제라면 여기 제로보드에서도 비정상으로 나타나야 합니다.
아니면 IE8 문제일까요?
IE8이 문제라면 여기 제로보드에서도 비정상으로 나타나야 합니다.
네이버 블로그나 카페에서도 이상이 없습니다.
따지고 보면 제로보드로 만든 제 홈페이지에서만 문제를 일으킵니다.
그런데 위 소스는 이곳에서도 같은 문제가 나타납니다.
이것이 해결이 안 되면 테이블 <TD> 내에서 백그라운드 이미지 사용에는 문제가 있을 수 밖에 없습니다.
고수 여러분, 도와 주세요.
댓글 3
-
감로수
2009.08.12 23:03
-
한마디
2009.08.12 23:33
감로수님, 정상적으로 나타났습니다.
일단 한글 코드가 깨지기는 했지만,
제대로 나타났습니다.
밑에 것은 소스코드 편집기로 넣어서 나타낸 것입니다.
테이블이 깨지는 문제만 바로 잡으면 될 것 같은데
어떻게 하신 것인지 궁금합니다.
제가 코드를 좀 살펴 보겠습니다.
감사합니다.
KHM式 원자수리계산법의 특징
1. 셈방법이 종래의 필산법보다도 대단히 간편하고 빠르다.
숙달하면 할 수록 그 셈처리의 간편함과 빠른 속도에 놀라게 된다.
2. 체계적이고 일반적이어서 모든 실무상의 셈처리가 신속정확하다.
수리(數理)가 과학적으로 체계화(體系化)되고 일반화(一般化)되어 있는고로 가ㆍ감ㆍ승ㆍ제에 관한 모든 실무상의 계산을 거의(視覺)적으로 신속 정확하게 처리할 수가 있어서 현대인들에게는 없어서는 아니될 새로운 생활수단의 무기가 된다.
3. 보통 평범한 두뇌로 손쉽게 이해하고 숙달할 수가 있다.
보통평범한 사람으로 국민학교 졸업 이상의 셈능력만 있으면 누구나 손쉽게 이해할 수가 있고 충분히 숙달이 되면 마치 "전자두뇌"와도 같이 모든 셈처리의 명수(名手)가 된다.
4. 습득할 수록 흥미를 느끼게 되고 단시일 내에 숙달할 수가 있다.
누구나 이해하고 습득해 나갈 수록 수리의 단순함과 신비성(神秘性)에 더욱 흥미를 느끼게 되고 따라서 단시일(短時日) 내에 숙달할 수가 있다.
5. 주판이나 계산기보다 능률적이고 대중적이다.
주판을 수년간 습득하여도 불과 수주일(數週日) 간에 습득해서 숙달할 수 있는 이 셈법의 셈능륭을 따르기가 어렵고 취급이 까다롭고 값비싼 계산기보다도 대중적이다.
6.「KHM式 원자수리계산법」과 종래의 「필산법」과의 비교
「KHM式 원자수리계산법」과 종래의 「필산법」과의 비교
덧셈
KHM式 덧셈법은 종래의 덧셈법과 같이 수를 하나씩 일일이 더해 나가는 복잡한 셈 처리가 아니고 모든 덧셈문제에다 숫자 셋씩의 합이 20이 되는 수를 기본 형태로 정하고 이루어지는 「KHM式 덧셈九九」를 그 「적용법」에 따라서 적용해서 셈을 처리하게 하는 고로 그 「덧셈九九」를 수주일간 충분히 암송(暗誦)하고나서 그 「적용법]에 숙달이 되면 누구나 그 답을 거의 시각(視覺)적인 눈셈처리로 신속정확하게 산출해서 그 답 자리에다 직접 적어 나갈 수가 있어서 일예로 10 ~ 20개의 수를 불과 1.2초(秒) 이내에 더할 수가 있고, 또 통계수(統計數)와 같이 각 자리수의 더한 결과가 60 이상으로 되는 많은 수라도 단숨에 이를 더할 수가 있어서 종래의 덧셈법은 물론 수년간 습득한 「주산」이나 「전자(電子)계산기」와도 이 셈 능률을 따를 수가 없게 된다.
뺄셈
KHM式뺄셈법은 종래의 뺄셈법과 같이 각 자리마다 일일이 빼 나가다가 뺄 수가 없을 경우에는 그 윗자리에서 1을 빌려오는 복잡한 셈 처리가 아니고 모든 뺄셈 문제에다 한 자리씩을 기본 형태로 정하고 이루어지는 「KHM式뺄셈九九」를 그 「적용법」에 따라서 적용해 나감으로서 누구나 그 답을 거의 시각(視覺)적인 눈셈처리로 신속 정확하게 산출해서 그 답 자리에다 쏜살같이 빠르게 적어 나갈 수가 있어서 종래의 뺄셈법은 물론 어떠한 「계산기기(器機)」라도 이 셈속를 따를 수가 없게 된다.
곱셈
KHM式 곱셈법은 종래의 곱셈법과 같이 「곱하는 수」의 각 자리수를 「곱해주는 수」의 각 자리 수에다 일일이 방사(放射)식으로 곱해서 이를 각 자리 수에 따라서 모두 더해 나가는 복잡한 셈 처리가 아니고 모든 곱셈문제에다 「곱해지는 수」와 「곱하는 수」의 각각 두 자리씩을 기본 형태로 정하고 이루어지는 「KHM式 곱셈九九」를 그 「적용법」에 따라서 적용해 나감으로서 누구나 그 답을 간편하고 신속 정확하게 산출해서 그 답 자리에다 직접 적어 나갈 수가 있어서 「곱하는 수」의 자리 수가 많을수록 그 셈 처리과정(過程)이 더욱 복잡해지는 종래의 곱셈법과는 비교할 수가 없게 된다.
[보기]
[KHM式곱셈법]
[종래의 곱셈법]
27
X 5321
--------------------
143667
27
x 5321
--------------------
27
54
81
135
--------------------
143667
나눗셈
KHM式 나눗셈법은 종래의 나눗셈법과 같이 「나누어지는 수」를 「나누는 수」로 직접 각 자리 수에 따라서 일일이 나누어 나가는 복잡한 셈 처리가 아니고 모든 나눗셈 문제에다 나누는 수의 두 자리씩을 기본 형태로 정해서 이루어지는 「KHM式 나눗셈九九」를 그 「적용법」에 따라서 적용해 나감으로서 누구나 그 답을 식산(式算)형식으로 간편하고 신속 정확하게 산출해서 그 답 자리에다 직접 적어 나갈 수가 있어서 나누어지는 수의 자리수가 많을수록 그 셈 처리 과정이 더욱 복잡해지는 종래의 나눗셈법과는 비교할 수가 없게 된다.
[보기]
[KHM式 나눗셈법]
[종래의 나눗셈법]
7456269 / 29
= 257112...21
257112
29 )-----------
7456296
58
----
165
145
----
206
203
----
32
29
----
36
29
----
79
58
----
21
-
한마디
2009.08.12 23:34
홈페이지에 입력한 것입니다.
http://www.khm-method.com/xe/?mid=calculation
한글이 깨져 나왔습니다.
그러나 이미지 부분은 정상적으로 나왔습니다.
고생이 많으시네요
올려드린 파일로 다시한번 해보세요.